Voting Cycles And Arrow’s Paradox Essay ⋆ Political Science Essay Examples ⋆ EssayEmpire

The idea of democracy closely relates to the method by which group decisions are made and managed. In this sense, democracy relates to the rules that transform individual preferences into a group preference through voting. However, there are considerable differences between individual decisions and group decisions. While individual voters are rational, meaning that they have complete and transitive preferences, the collective choice—the aggregation of individual preferences—could end in intransitive results.

Marie Jean Nicolas Caritat, Marquis de Condorcet (1743– 1794), noted the irrationality of collective decisions that can originate from rational individuals. He demonstrated the possibility of an election becoming a paradox in which a corrupt triangle, or voting cycle, could be formed with no winner. For instance, if A beats B, B defeats C, and C beats A, the collective ranking is circular, creating a paradox in which no candidate obtains a clear majority.

Figure 1

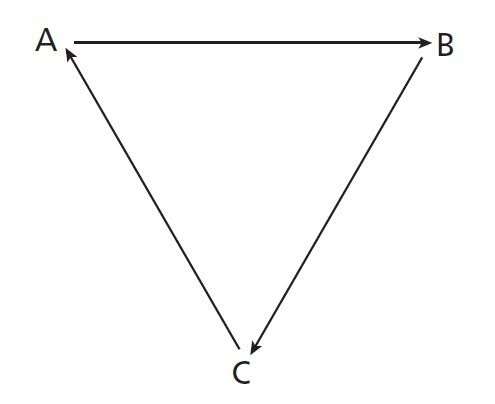
Voting Cycles And Arrow’s Paradox Essay

For example, three individuals (1, 2, and 3) are deciding on three alternatives (A, B, and C). Their order of preferences is as follows:

Individual 1: A > B > C

Individual 2: B > C > A

Individual 3: C > A > B

Individual 1 prefers alternative A rather than B, B rather than C, and consequently, A rather than C. The same logic applied to the other individuals. For this reason, individuals 1, 2, and 3 are rational. Nonetheless, following Condorcet’s rule, as a group decision, any alternative could be the winner. The result is a paradox.

The one candidate who should win is the one who can top each of the others, as was the case in South Korea’s 1987 presidential election. Voters chose between several candidates, but none received the majority of the vote (50 percent plus one). Instead, Roh Tae Woo won the election with a plurality of 36.6 percent, more than any other candidate, but far short of a true majority of all votes. Barring a plurality, a voting cycle may be broken by a runoff election.

Condorcet demonstrates that it may become difficult and even impossible to learn the opinion of a group through the vote of individuals. Paradoxical results may be due to the intransitivity of opinions from individuals to groups. It is important to note that intransitivity may occur in the collective decision, but not in the individual decision. Transitivity is an important condition that provides coherence to the individual decision-making process.

In a voting cycle, it is possible that no candidate clearly wins an election. All the combinations of plural voting (i.e., choice among several) or majority voting (i.e., choice among a pair, or successive pairs) may present defects or voting cycles. The voting methods used that result in voting cycles often produce no result or unfair, defective, or corrupt results.

Jean Charles de Borda (1733–1799) suggested the consensus-based voting system to avoid such failure. Supposedly it could avoid voting cycles because it combines plural voting with a double-rating system in which not only the result of the voting is considered but also a rating according to the grade in scale of majority—first, second, and third candidate would have successive less rating besides the voting result. Thus the voter is asked to rank candidates in order of preference and this preference is combined to the rank majority pointed.

Voting cycles were more recently better formulated and analyzed by Kenneth Arrow, 1972 Nobel Prize winner in Economic Sciences. In 1951, Arrow sets five postulates to all democratic regimes: universality, citizen sovereignty, nondictatorship, positive association of social and individual values, and restriction of irrelevant alternatives. The postulates are considered reasonable for collective decision making that takes, as its basis, individual preferences expressed by voting. Arrow’s paradox is also called an axiom since, once compliance is achieved with the five postulates, the voting method used becomes irrelevant; any method would work fairly, but none perfectly. In this sense, Arrow also demonstrates that it is impossible to have the majority desire to prevail without breaking at least one of the postulates.

Voting cycles and Arrow’s paradox also connect directly to the importance of holding the agenda power in legislatures or other decision-making bodies. In theory, if the person that builds the agenda knows individuals’ preferences on different issues, the agenda could be manipulated in order to achieve a winner that might not represent the collective desire.

Bibliography:

Arrow, Kenneth. Social Choice and Individual Values. New York: Wiley, 1951.
Condorcet, Jean-Antoine Nicolas de Caritat, Marquis de. Essai sur l’application de l’analyse à la probabilité des décisions rendues à la pluralité des voix. Paris: De l’Imprimerie Royale, 1785.
Gehrlein, William V. Condorcet’s Paradox. Berlin: Springer, 2006.
Nurmi, Hannu. Voting Procedures under Uncertainty. Berlin: Springer, 2002.
Tabarrok, Alexander. “Paradoxes of Voting.” Paper, Department of Economics, George Mason University, February 8, 2005.

This example Voting Cycles And Arrow’s Paradox Essay is published for educational and informational purposes only. If you need a custom essay or research paper on this topic please use our writing services. EssayEmpire.com offers reliable custom essay writing services that can help you to receive high grades and impress your professors with the quality of each essay or research paper you hand in.